前回のページからの続きです。
前回のまとめ
実際の数値だけの記録では正確な情報を財務諸表利用者に届けられない!
ということで実効金利という概念が生まれたのでした。
それでは例題を通して、実効金利の概念や考え方や仕訳に慣れましょう。
実効金利法の例題:社債
解法
社債が発行されるという事は「Dr. Cash / Cr. Bond payable」の仕訳が発生し、差額が「Bond premium or Bond discount」になる、という大原則を仕訳として表現する事が第1歩となります。
Bond payable は単純な発行額面で良いので簡単です。答えは10,000です。
問題は手元に入ってくるCashがいくらになるか、です。
そしてこの手元に入ってくるCash=帳簿価額(Carrying Amount)と呼びます。
実効金利法では帳簿価額(Carrying Amount)と額面価額(Face Amount)が重要になります。
この現在価値をどのようにして計算するか、一般的には計算式を用いて計算しますが試験本番では時間短縮の為、現価係数と年金現価係数の表が与えられます。
例題では簡略化の為、初めから正解の係数を記載しましたが、本番では表から自分で正しい係数を探し出す必要があります。ここでは与えられた係数を使用して下さい。
では「社債額面10,000の現在価値+満期までに発生する金利の合計額の現在価値」を計算しましょう。
現価係数
読んで字の如く、現在の価値計算に使用する係数です。(現価係数の誤字に注意!『原価』係数と表記していると意味が分かりづらくなります)
2021年1月1日に発行して受け取った10,000は、満期である5年後の2026年1月1日に債権者へ返却する必要があります。
つまり2026年1月1日に返済する負債10,000は2021年1月1日時点でいくらの価値になるのか
を計算する為に現価係数を使用します。
10,000×0.82035≒8,204
という事でまずは2026年12月31にに返済する負債10,000は実行利率4%のこの例題に於いては、2021年1月1日時点で8,204の価値となります。
年金現価係数
現価係数に「年金」が付くと、年金現価係数という単語になります。
年金とはもともと「一定期間にわたり、定期的に支給される金銭」という意味です。
一定期間受け取る事が決まっている定期支給金銭の合計額を、現時点の金銭価値に換算するといくらになるか、を計算するための係数となります。
したがって社債の現在価値を計算する際の「満期までに発生する金利の合計額の現在価値」部分を計算する際に使用する係数です。
より正確には、2021年6月30日・2021年12月31日・2022年6月30日・2022年12月31日・2023年6月30日・2023年12月31日・2024年6月30日・2024年12月31日・2025年6月30日・2025年12月31日に、額面10,000×(表面利率6%÷2)=300ずつの金銭支給を受け取る事が出来ます。
表面利率6%÷2の記載についての理解は大丈夫でしょうか。年率6%且つ支払は年2回で満期5年である為、半年に1回年率3%の支払が満期までに10回発生する、という解釈になります。
この点に関して私自身は悩まずにすんなりと理解が出来、周囲の合格者でもこの点に違和感を覚えたという人には出会ったことがないのですが、もし「?」となる場合は、「そういうもの」だと割り切った方が良いかと思います(現価係数の深堀をすれば解説は出来るのですが、あまりにも時間が掛かり試験の本質ではない論点なので割愛します)
参考までに「満期5年、表面利率6%、金利支払いは毎年12月31日の年1回」の場合は、1年に1回年率6%の支払が満期までに5回発生する、という解釈になります。
では年金現価係数を用いて金利の現在価値を計算してみましょう。
300×8.98259≒2,695
年金現価係数を用いる場合、「1期間で貰える金銭×年金現価係数」の計算となります。
慣れないうちは金銭合計額(300×10期間)等を用いてしまいがちなので、問題を解いて慣れましょう。
本来の意味である「一定期間にわたり、定期的に支給される金銭」の現在価値を計算する、と理解しておけば「定期的に支給される金銭(半年に1度、300)」が主役であると理解しやすいかと思いますのでしっかりと元の意味から理解しましょう。
例題:社債の解答
それでは例題を解いていきましょう。
発行時
まずは社債発行時の仕訳について
参考ですが、試験で直接発行時仕訳が問われていなくても、経過(金利支払い時、会計期末時点)や償還時の仕訳や数字が問われている場合、発行時仕訳が理解出来ていないと解けません。
ここに関しては問題演習、模擬試験、何なら試験本番でも問われているいないにかかわらず、発行時仕訳を書いた方が良いです。
それでは大事な発行時仕訳を解きます。
大前提ですが、上でも書いた通り「Dr.cash、Cr.負債、差額があればdiscount or premium」が基本です。というか試験ではこのパターン以外出ません。
そしてCr.負債は簡単で、問題文にある額面10,000がそのまま回答です。
難しいのはDr.cashです。
額面10,000の計上が楽でいいじゃん、と思うかもしれませんがここは会計学のポイントです。
表面金利と実効金利が相違している場合、必ず社債価格=Dr.cash金額は、Cr.負債と相違します。
このリスク差や金利差が勘案されて、社債価格は決定されます。
上記の通り「社債額面10,000の現在価値+満期までに発生する金利の合計額の現在価値」が社債価格となります。
10,000×0.82035≒8,204
300×8.98259≒2,695
社債の現在価値=社債額面10,000の現在価値8,204+満期までに発生する金利の合計額の現在価値2,695=10,899
したがってDr.cash=10,899となり、Crに差額899を記入すると貸借が一致します。
この差額、Cr側に来ているのでBond Premiumですね。
もし「あれ、差額でどっちがDiscountでどっちがPremiumだっけ」とド忘れしても、
と考えると、「この社債は人気だから多少のプレミアムを付けて定価10,000より高く設定しても売れるな」という社債発行者の声が聞こえてきそうです。
このストーリーからも今回の差額899がBond premiumだと理解できるのではないでしょうか。

Dr.の10,899が帳簿価額(Carrying Amount)
Cr.の10,000が額面(Face Amount)
実際に支払われる金利は「額面Face Amount × 表面利率」
会計上の数字把握目的で計上する金利は「帳簿価額Carrying Amount × 実効金利」
この2つの金利を併用する記録方法が実効金利法
具体的に以下で確認していきましょう。
2021年6月30日
この日の仕訳を切ります。第1回目の金利支払いですね。
金利支払いもベースは単純で、投資家へ支払うからcashが出て行き(Cr.cash)、負債返却とは別の金利という利息支払が発生する(Dr.Interest expense)、差額はDiscount or Premiumの調整(満期に向けて、Discount or premiumは縮小していき、満期日に額面と負債が等しくなる為金利支払いのタイミングでDiscount or premiumを小さくする)
この差額を小さくする、というのが実効金利法の肝です。
この例題で言うと、発行時のBond Premium 899は満期である5年をかけて、0になります。
具体的には金利支払い300、金利費用(10,899×4%÷2≒218)、差額(300-218=82)がBond Premiumの2021年1月1日~2021年6月30日の縮小分となります。

2021年12月31日
直近の利払い日2021年6月30日の仕訳でBond premiumが82減少しています。
2021年12月31日のInterest expenseを計算する際にはこの82の減少加味を忘れないでください。
(10,899-82)×4%÷2≒216
2021年12月31日の金利費用は216となります。
支払で出て行くキャッシュは300で一定である為、差額(300-216)84が2021年12月31日時点のBond Premiumの減少額となります。
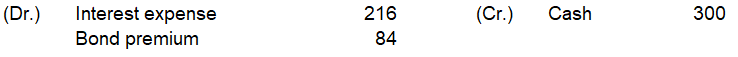
【参考】満期までの各利払い日の仕訳
発行時に発生したBond discount / premium は満期に向けて縮小していき、満期時にはゼロになります。
この例題を通して、2022年6月30日、2022年12月31日、2023年6月30日、2023年12月31日、2024年6月30日、2024年12月31日、2025年6月30日、2025年12月31日の仕訳を見ておきましょう。
ポイントはBond premiumが縮小していく過程と、縮小したpremiumの分だけ金利費用が減少していく過程の2点です。
より具体的には、発行時にCrに計上されたBond premiumが、利払い日毎にBond premiumが反対側のCrに計上される事で相殺されていき、縮小していく=反対側であるCr計上額が大きくなっていく、という事です。
2022年6月30日
計算は以下です
(10,899-82-84)×4%÷2≒215
300-215=85
仕訳は以下です
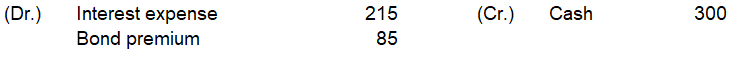
2022年12月31日
計算は以下です
(10,899-82-84-85)×4%÷2≒213
300-213=87
仕訳は以下です
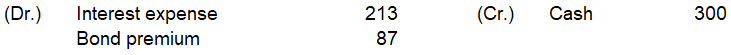
2023年6月30日
計算は以下です
(10,899-82-84-85-87)×4%÷2≒211
300-211=89
仕訳は以下です
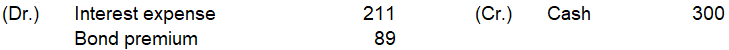
2023年12月31日
計算は以下です
(10,899-82-84-85-87-89)×4%÷2≒209
300-209=91
仕訳は以下です
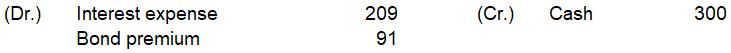
2024年6月30日
計算は以下です
(10,899-82-84-85-87-89-91)×4%÷2≒208
300-208=92
仕訳は以下です
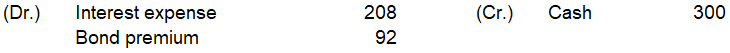
2024年12月31日
計算は以下です
(10,899-82-84-85-87-89-91-92)×4%÷2≒206
300-206=94
仕訳は以下です
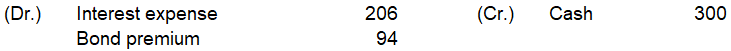
2025年6月30日
計算は以下です
(10,899-82-84-85-87-89-91-92-94)×4%÷2≒204
300-204=96
仕訳は以下です
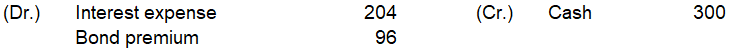
2025年12月31日
計算は以下です
(10,899-82-84-85-87-89-91-92-94-96)×4%÷2≒204
300-204=96
仕訳は以下です
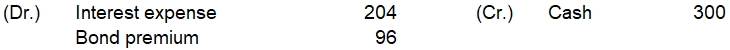
満期
満期時点の帳簿価額(Carrying Amount)
(10,899-82-84-85-87-89-91-92-94-96-96)=10,003
※小数点以下四捨五入しているため差額3が発生していますが、正確に計算すると10,000となります。以下仕訳では便宜上10,000を用います。
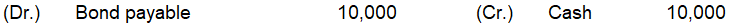
最後に
金利支払いが登場する場合、表面金利と実効金利の概念が必ず絡むと認識して下さい。
とは言っても具体的にはほぼ「社債」と「リース」の2分野です。
FAR試験で「社債もリースもどちらも出題されない」という状況はありえないので実効金利法が苦手な方は概念の理解を進めながら、問題を解きまくって慣れていきましょう。













